Symmetry, Flatness, and Constancy

This test characterizes the beam's general shape. It starts by sampling the image in 5 circles , (whose positions are corrected for collimator centering) as shown in the following image and reporting them in CU (Calibrated Units) Click image to enlarge:

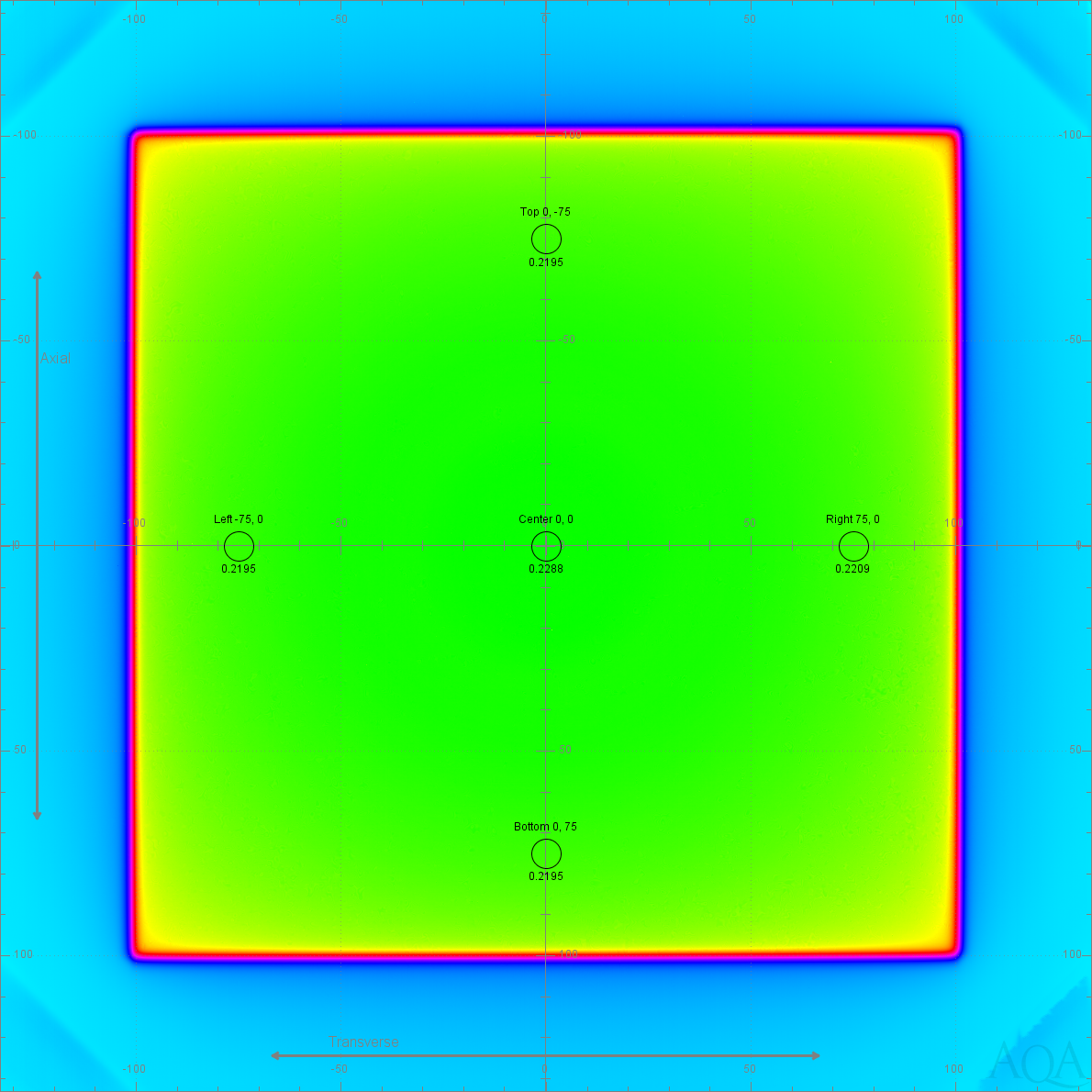
Each circle is 5 mm in diameter. They are 75 mm from the center of the image, with a compensation for collimator centering.

For the examples, the following values are used:

Inputs

Source	Top CU	Bottom CU	Left CU	Right CU	Center CU
Analysis	0.2195	0.2195	0.2195	0.2209	0.2288
Baseline	0.2206	0.2209	0.2220	0.2210	0.2301

Note on baseline values: Some tests are better evaluated when they can be compared to previous values. For these tests, AQA allows users to establish baseline values. When a test is run, the results are compared to the baseline values. The first time a test is run there are no baseline values, so the platform uses the results of the current test to establish them.

Users may override this default by using the "Use As Baseline" button, which will establish a new baseline going forward.:w

Calculation of Symmetry

Symmetry is calculated both axially and transversely as a percentage with:

axial      = ((top   - bottom) / bottom) * 100

transverse = ((right - left  ) / left  ) * 100

As an example, using the the above diagram:

axial      = ((0.2195 - 0.2195) / 0.2195) * 100 = 0.0

transverse = ((0.2209 - 0.2195) / 0.2195) * 100 = 0.6378

Calculation of Flatness

Flatness is calculated over the image as a percentage using the maximum and minimum values of the 5 measured circles:

(max - min) / (max + min) * 100

As an example, using the the above diagram:

flatness = ((0.2288 - 0.2195) / (0.2288 + 0.2195)) * 100 = 2.0745

Calculation of Constancy

Constancy is calculated over the image by dividing each of the outer values by the center value then subtracting each from the baseline values, processed similarly:

t = (top    / center) - (baseline top    / baseline center)

b = (bottom / center) - (baseline bottom / baseline center)

l = (left   / center) - (baseline left   / baseline center)

r = (right  / center) - (baseline right  / baseline center)

The sum of these is taken, multiplied by 100 and averaged:

((t + r + b + l) * 100) / 4

An example, using the the above values:

t = (0.2195 / 0.2288) - (0.2206 / 0.2301) =  0.0006395

b = (0.2195 / 0.2288) - (0.2209 / 0.2301) = -0.0006642

l = (0.2195 / 0.2288) - (0.2220 / 0.2301) = -0.0054450

r = (0.2209 / 0.2288) - (0.2210 / 0.2301) =  0.0050200

((0.0006395 + -0.0006642 + -0.0054450 + 0.0050200) * 100) / 4 = -0.01124

Image Noise

The standard deviation is recorded for each of the five circles as a measurement of image noisiness. If this value is large it indicates a poorer image quality. To normalize noisiness for comparison between beams and machines, the value is displayed as the coefficient of variation, which is:

coefficient of variation = standard deviation / mean

An example, using the the above center value and a standard deviation of 0.0002643:

0.001155 = 0.0002643 / 0.2288